Удивительно, но мы, мужчины, гораздо с большей ответственностью относимся к выбору автомобиля, или мобильника, чем к выбору жены! И это притом, что автомобиль мы выбираем на 3-5 лет, а жену на всю жизнь! Мы тщательно изучаем авто-каталоги, интересуемся техническими характеристиками, расспрашиваем знакомых и экспертов о возможных дефектах и т.д. Затем включаем логику, анализ, калькулируем бюджет и, наконец, принимаем решение. Женщины аналогично выбирают сумочки, кофточки и прочее, применяя самые сложные аналитические механизмы, о которых мы даже не догадываемся.
А вот когда надо выбрать жену (или мужа) — все происходит по-другому: логики вообще нет, аналитика если и присутствует, то строится на неподтвержденных данных — одни эмоции… называем это Любовью, чтобы снять с себя ответственность! Поразительно, но так оно и есть. Не всегда, конечно же, но очень часто. И все мои усилия, дорогой читатель, направлены на то, чтобы ты не оказался в числе той самой безответственной половины мужско-женского населения.
Итак, в математических терминах нашу задачу можно сформулировать следующим образом:
из ограниченного множества невест
{Xi}, где 0 < i ≤ N,
обладающих определенным набором параметров (качеств)
nj , где nimin ≤ ni ≤ nimax ,
требуется выбрать одну невесту, с идеальными параметрами { niид ±δi }.
Введем также следующее ограничение: если ты перебираешь невест одну за другой, то возврата назад, к тем которых ты отверг, уже нет (в жизни чаще всего именно так и бывает).
Очевидно, что прежде, чем приступить к решению задачи, нужно уточнить само условие, а именно: чему равны — N, nimin , nimax, niид и δi. И главное, предложить план (стратегию) поиска.
Поясню нашу задачу на простом и понятном примере. Представь, что ты отправился в туристический поход по маршруту «Золотая Индигирка», который пролегает по местам добычи золота в Оймяконском улусе в Якутии. Сейчас такие туристические маршруты становятся популярными и организованы в Австралии и Финляндии, например. В России тоже этот увлекательный вид туризма начинает развиваться. Итак, туристов доставили к живописному ручью с золотоносным песком, снабдили соответствующим инвентарем и поставили условие: ты можешь забрать себе только один слиток. Как только ты принимаешь решение, что забираешь очередной из найденных слитков, то на этом твой дальнейший поиск прекращается. Если ты решаешь продолжить поиск, то последний найденный тобой слиток поступает в пользу государства, и забрать его ты уже не можешь.
В таких условиях, каждый раз, когда ты находишь золотой слиток, необходимо принять решение, забрать или продолжать искать дальше? При этом любое твое решение может оказаться ошибочным. Например, ты решаешь забрать, полагая, что найденный тобой слиток достаточно большой. А на самом деле, если бы ты продолжил поиск, то нашел бы ещё больший. Но если ты решишь продолжить поиск, то тоже можешь ошибиться, так как все остальные найденные тобой слитки могут оказаться гораздо меньше того, который ты уже передал в государственный золотой запас. Математики называют эти ошибки так: «ошибка 1-го рода» и «ошибка 2-го рода». При этом ошибкой 1-го рода называется та, которая менее желательна. Что именно для тебя менее желательно: пропустить самый крупный слиток или выбрать не самый крупный – решать тебе. Если ты выбираешь не золотой слиток, а невесту, то женитьба на далеко не самом лучшем варианте, пожалуй, менее желательна, чем пропуск самого-самого лучшего. Поэтому, выбор неудачного варианта будет ошибкой 1-го рода, а пропуск удачного – ошибкой 2-го рода. Вернемся к нашему золотоносному ручью и (по аналогии с выбором невесты) определимся, что ошибкой 1-го рода будет для нас выбор далеко не самого большого самородка, а пропуск самого большого – ошибкой 2-го рода. Наша задача – снизить к минимуму вероятность ошибки 1-го рода!
Итак, ты берешь свои инструменты – кирку, лопату и лоток, и приступаешь к работе. Проходит 10, минут, 20, час и… о радость! Первый слиток! Взвешиваешь — 10 граммов! И… начинаешь мучиться: брать или не брать? Но, поскольку для тебя более важно не остановиться на самом маленьком слитке, то ты принимаешь решение продолжать поиски. Проходит ещё час и ты находишь второй слиток – 8 граммов. Так, у тебя появились первые статистические данные. Во-первых, ты можешь предположить, что в среднем раз в час будешь находить по одному слитку. Вам разрешили работать с 9-00 до 19-00, десять часов, значит, всего ты можешь найти десять слитков (N = 10). Во-вторых, ты можешь оценить средний вес слитков, которые «водятся» в этом ручье: (10 + 8)/2=9 граммов. Но, конечно, выборка из двух элементов, слишком маленькая для статистики. И ты принимаешь такое решение: половину возможностей, то есть первые пять слитков (N/2 = 5), пропустить, после чего забрать первый слиток, вес которого окажется больше всех предыдущих. Ты продолжаешь намывать золото и находишь еще 3 слитка. Веса найденных слитков представлены в таблице 2.1.1.
| номер слитка | 1 | 2 | 3 | 4 | 5 |
| вес, г | 10 | 8 | 12 | 6 | 9 |
Табл.2.1.1. Вес найденных слитков в порядке их нахождения.
Полученная статистика дает возможность оценить желаемый для тебя результат. Конечно, ты бы хотел найти слиток весом в 100 граммов, но, если полагаться на имеющиеся статистические данные, то находка слитка весом более 12 граммов будет для тебя и предпочтительной, и реальной.
После этого небольшого аналитического исследования статистических данных ты продолжаешь свой старательский процесс: 6-й слиток – 9 граммов, 7-й слиток – 11 граммов, 8-й слиток — 13 граммов. Стоп! Процесс закончен. Уставший, но довольный ты возвращаешься в посёлок старателей, но ночью не можешь уснуть. Тебя продолжает мучить один и тот же вопрос: самый крупный самородок ты забрал или нет? У математиков есть ответ на твой вопрос: вероятность того, что тебе достался самый крупный из 10 ( N = 10) возможных самородков равна 25%. И эта вероятность при данной стратегии не зависит от N! Теперь ты можешь спать спокойно. Неопределенности больше нет. Если ты будешь работать четыре дня, и каждый раз применять эту стратегию, то в один из дней тебе достанется самый большой самородок, а в другие три дня не самый большой, но и не самый маленький. Совсем не плохо! Но математики говорят, что эту стратегию можно улучшить. А именно, оптимальной стратегией будет такая: ты пропускаешь первые s экземпляров, где s определяется двойным неравенством:
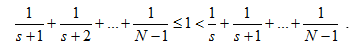
В этом случае, для нашей старательской стратегии при N = 10 оптимальным будет пропуск трех первых слитков ( s = 3), а затем уже выбор первого из оставшихся, который больше любого из трех первых. При этом вероятность выбрать наибольший из всех десяти ≈ 0,4 (40%). Замечу, на будущее, что если N растет, то эта вероятность стремится к 1/е, где е – основание натурального логарифма, то есть к значению ≈ 0,37 (37%).
Вернемся к нашей задаче выбора невесты. В отличие от задачи с золотыми слитками задача выбора жены несколько сложнее, так как у нас теперь не один параметр (вес золотого слитка в граммах), а гораздо больше (внешность, рост, вес, возраст, образование, воспитание, характер, прописка, приданое, и так далее). Но суть одна и та же, поэтому мы применим ту же самую оптимальную стратегию, которая описана выше для выбора золотого слитка. Первый вопрос, который возникает, как оценить N — количество потенциальных невест. Это количество зависит от твоего темперамента, коммуникабельности и реального желания найти жену. Предположим, тебе 20 лет, ты решил жениться до 30 и в среднем у тебя получается знакомиться с новой девушкой один раз в месяц, то есть 12 раз за год. В рамках указанных допущений, количество твоих потенциальных невест равно 120-ти:
N = 10 ∙ 12 = 120
Конечно, у всех мужчин способности знакомиться с девушками разные. Да и у тебя с возрастом этот навык будет совершенствоваться. Через год другой ты увидишь реальные свои успехи и сможешь заново пересчитать все исходные значения, которые мы получим, но пока нам надо на чем-то остановиться. Итак, если ты потенциально сможешь познакомиться с N = 120 девушками претендентками на роль будущей жены, то количество девушек которых ты должен «пропустить» для статистики s = 32 (это я подсчитал, чтобы тебя не утруждать расчетами), но ты можешь убедиться в этом и самостоятельно, например, простым подбором значений, подставляя их в приведенные выше неравенства.
Итак, первых 32-х девушек ты должен пропустить просто для статистики, для уменьшения вероятности ошибки первого рода, так сказать. Постарайся в этот период сильно не влюбляться, не давать волю эмоциям и не пудрить мозги девушкам (не легко, но уж постарайся!). Твоя задача на этом этапе – набрать статистику значений параметров невест из твоего множества (всего 120 потенциальных кандидатур) и разобраться в себе: удовлетворяют тебя те значения функции идеальной жены, которые получены в результате этой начальной выборки из 32-х кандидатур или нет.
Вперед!
